2^n/3^n converge or diverge 255888-Does (2/3)^n converge or diverge

Use the divergence test to determine whether a series converges or diverges Use the integral test to determine the convergence of a series Estimate the value of a series by finding bounds on its remainder term In the previous section, we determined the convergence or divergence of several series by explicitly calculating the limit of the Show Solution To determine if the series is convergent we first need to get our hands on a formula for the general term in the sequence of partial sums s n = n ∑ i = 1 i s n = ∑ i = 1 n i This is a known series and its value can be shown to be, s n = n ∑ i = 1 i = n ( n 1) 2 s n = ∑ i = 1 n i = n ( n 1) 2 Sequences Convergence and Divergence In Section 21, we consider (infinite) sequences, limits of sequences, and bounded and monotonic sequences of real numbers In addition to certain basic properties of convergent sequences, we also study divergent sequences and in particular, sequences that tend to positive or negative infinity We

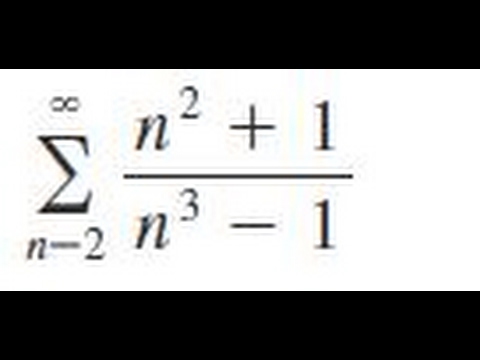
Sigma 2 Infinity N 2 1 N 3 1 Determine Whether The Series Converges Or Diverges Youtube

Does (2/3)^n converge or diverge

Does (2/3)^n converge or diverge-Diverges, LCT with P 1 n which diverges, or directly compare 2n1 3n24 2n 3 2 = 1 2n and 1 2 P 1 n diverges (f) X 1 ( 1)n n diverges, Test for Divergence 4Determine if the following series absolutely converge, conditionally converge, or diverge (a) X sinn n2 1 converges absolutely, direct comparison 0 jsinn n21 j 1 and P 12Determine if the following series converge or diverge You must show all of your work and justify your use of any series convergence tests (a)(7 points) X1 n=1 n3 3n Solution Consider the ratio test lim n!1 (n 1)3 3n1 3n n3 = lim n!1 (n 1)3 n3 3n 3n1 = 1 1 3 = 1 3 Since this limit L

Calculus Sum Of 1 To Infinity Of Ln N Sqrt N Convergent Or Divergent Learnmath

The sequence diverges 3 X∞ n=2 n2 1 n3 −1 The terms of the sum go to zero, since there is an n2 in the numerator, and n3 in the denominator In fact, it looks like P 1 n, so we compare it to that lim n→∞ n2−1 n3−1 1 n = lim n→∞ n3 −n n3 −1 = 1 Therefore, the series diverges by the limit comparison test, with P 1 n 4 X∞ n=1 5−2 √ n n3531 Use the divergence test to determine whether a series converges or diverges 532 Use the integral test to determine the convergence of a series 533 Estimate the value of a series by finding bounds on its remainder term In the previous section, we determined the convergence or divergence of several series by explicitly calculatingConverge or both diverge lim 0n n n a c c →∞ b n=2 n=3 n=4 n=5 n=6 n=7 n=8 Is the alternating sequence converging?

Give reasons for your answers (When you check an answer, remember that there may be more than one way to determine the series' convergence or divergence) $$ \sum_{n=1}^{\infty} \frac{2^{n}}{3^{n}} $$ In order to converge, the limit of the terms of the sequence must approach 0;Let a n = 2 n 3 n 1 (a) Determine whether {a n} is convergent (b) Is ∞ X n =1 a n is convergent?

Ask Question Asked 8 years, 3 months ago Active 8 years, 3 months ago Viewed 43k times 13 7 $\begingroup$ so I used the root test, but i'm not quite sure if i'm allowed to I think im performing the operations correctly,a and i keep ending up with $(1)^{\infty}$Thus the series on the left diverges as well, and adding back in the finite number of terms for n < N does not affect the result Thus ∞ n = 2 1 (ln n) 4 diverges 62 ∞ n = 1 2 n 3 n − n solution Apply the Limit Comparison Test with a n = 2 n 3 n − n and b n = 2 n 3 n L = lim n →∞ a n b n = lim n →∞ 2 n 3 n − n 2 n 3 n = limFor convergence or divergence Solution We have a n = 2n 3n 1 n→∞ a n b n = c, and if 0 < c < ∞, then either both series converge or both diverge The limit comparison test follows from the basic comparison test Indeed, we may choose two real

What Is The Radius Of Convergence On The Power Series From 0 To The Infinity Of 1 N 3 N 2 N X N Quora

Geometric Series Test To Figure Out Convergence Krista King Math Online Math Tutor

Explain your answer X1 n=1 n 3n Answer Use the Ratio Test lim n!1 n1 3n1 n 3n = lim n!1 n 1 3n1 3n n = lim n!1 1 3 n 1 n = 1 3 Since 1 3Converge or Diverge?—Comparison and Limit Comparison Learning goal Students start to use more convergence tests—comparison and limit comparison tests are introduced, and pseries are used as the basis for many comparisons For what values of p does the series 1 np n=1 ∞ ∑ converge? Does the series converge or diverge?

Answered Does The Sequence An Converge Or Bartleby

Http Dept Math Lsa Umich Edu Zieve 116 Series2 Solutions Pdf

Lim n → ∞ (2 n 1) / 3 n 2 n / 3 n = 1 lim n → ∞ (2 n 1) / 3 n 2 n / 3 n = 1 Since ∑ n = 1 ∞ ( 2 3 ) n ∑ n = 1 ∞ ( 2 3 ) n converges, we conclude that ∑ n = 1 ∞ 2 As you correctly note, this is e 3 − 1 That's because the series for e x converges everywhere!So you are done, it converges (specifically to e 3 − 1 ) When saying that you have 'reduced it' to e 3 − 1 which none the less is correct and thus the series converges to that particular value you most likely used that e x = ∑ n x n / n

Calculus Sum Of 1 To Infinity Of Ln N Sqrt N Convergent Or Divergent Learnmath

Will Series N N 1 Converge Or Diverge As N Tends To Infinity Quora

To converge Similarly, a given improper integral diverges if its integrand is greater than the integrand of another integral known to diverge We now apply the same idea to infinite series instead Direct Comparison Test for Series If 0 ≤ a n ≤ b n for all n ≥ N, for some N, then, 1 If X∞ n=1 b n converges, then so does X∞ n=1 a nAnswer to Does this series converge or diverge?This sum divergeswe can say this by using the pseries theorem eg we have a series summation (n^p) where n goes from 1 to infinity then if p>1 then the series converges and if p

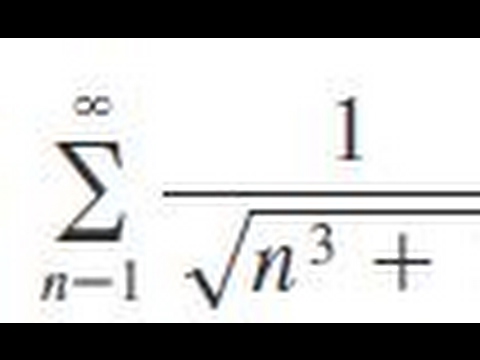
Sigma 1 Infinity 1 Sqrt N 3 1 Determine Whether The Series Converges Or Diverges Youtube

Www3 Nd Edu Dgalvin1 S08 Exam3 Solns Pdf

Proof If p 1, the series diverges by comparing it with the harmonic series which we already know diverges Now suppose that p>1 The function f(x) = 1=xp is a decreasing function, so to determine the convergence of the series we'll detemine the convergence of the corresponding integral Z 1 1 1 xp = 1 (p 1)xp 1 1 1 = 0 1 p 1 Determining convergence (or divergence) of a sequence Convergence means that the infinite limit exists If we say that a sequence converges, it means that the limit of the sequence exists as n → ∞ n\to\infty n → ∞ If the limit of the sequence as n → ∞ n\to\infty n → ∞ does not exist, we say that the sequence divergesThe sequence is for n ∈ ℕ divergent all right If we take the quotiënt of the functions f (n)=2^n and g (n)=n², and than use L'Hôpital's rule two times, we arrive at lim n → ∞ (ln (2))²^ (n1)=∞ L'Hôpital's rule Also let f (n)/g (n)=log f (n)/log g (n)=log 2^n/log n²=n*log 2/2 log n=

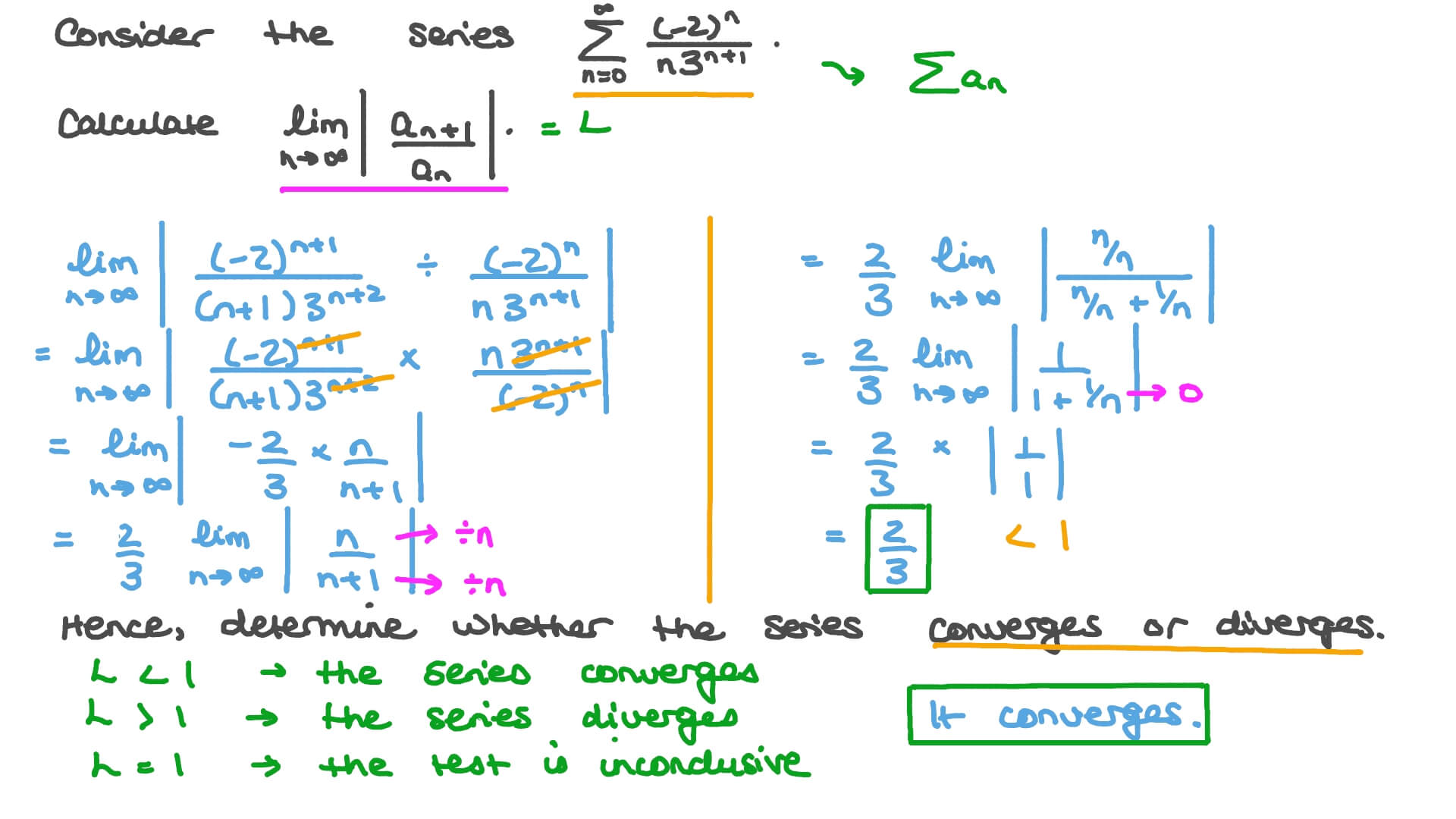
Question Video Using The Ratio Test To Determine Convergence Nagwa

Teachingcenter Ufl Edu Files Exam 2 Review Problems Mac 2312 Pdf

 The Divergence Test is a method used to determine whether the sum of a series diverges, and if it does, it is impossible to converge If the series does not diverge, then the test is inconclusive Take note that the divergence test is not a test for convergence We have learned that if a series converges, then the summed sequence's terms mustConvergence & divergence of geometric series In this section, we will take a look at the convergence and divergence of geometric series We've learned about geometric sequences in high school, but in this lesson we will formally introduce it as a series and determine if the series is divergent or convergentA necessary and sufficient condition for the convergence of a sequence is that it is bounded and has a unique limit point math2^n=(11)^n\ge 1n,\,\,\forall\,\,n\,\,\in\,\,\mathbb

Why Does It Matter What Convergence Test I Use Physics Forums

Find The Sum Of The Convergent Series Chegg Com

N2en = 1 and so lim n!1 ( 1)n(n1)!N diverges (b)The Nth partial sum of the series P 1 n=1 a n is S N = a 1 a 2 a N For example, take the infinite series defined by a n = 1 for all n Then a N = 1 but the Nth partial sum is N (c)If the general term a n tends to zero, the series may or may not converge See part (a) for an example (d)If L 6=0, then the series divergesWell, we should compare to the integral dx xp 1 ⌠∞ ⌡

Using The Integral Test For Series Convergence Study Com

Nth Geometric And Telescoping Test Ppt Download

Tests for Convergence of Series 1) Use the comparison test to con rm the statements in the following exercises 1 P 1 n=4 1diverges, so P 1 n=4 3 diverges Answer Let a n = 1=(n 3), for n 4 Since n 3 1=n, so a n > 1 n The harmonic series P 1 n=4 1diverges, so the comparison test tells us that the series P 1 n=4 3 alsoIt has a sumSince the sum of 3 diverges, and the sum of 1/2^n converges, the series diverges You have to be careful here, though if you get a sum of two diverging series, occasionally they will cancel each other out and the result will converge If the power is n1 or such, then factor out terms until you just have an n power

I Don T Understand This Explanation For Sum N 0 Infty 1 N 5n 1 Why Test For Convergence Divergence Again If The Limit Comparison Test Confirms That Both Series Are The Same Socratic

Calculus Find The Radius Of Convergence For 3n Online Presentation

S for some S then we say that the series P1 n=1 an converges to S If (Sn) does not converge then we say that the series P1 n=1 an diverges Examples 1 P1 n=1 log(n1 n) diverges because Sn = log(n1) 2 P1 n=1 1 n(n1) converges because Sn = 1¡ 1 n1!Grows much faster than n2en so lim n!1 (n1)!2 11 points Determine the convergence or divergence of the following series In parts (a) and (b), support your answers by stating and properly justifying any test(s), facts or computations you use to prove convergence or divergence Circle your final answer Show all your work a 3 points X∞ n=1 9n e−nn CONVERGES DIVERGES Solution

Teachingcenter Ufl Edu Files Exam 2 Review Problems Mac 2312 Pdf

Http Www Webassign Net Latex2pdf 0a7e1dfd215bf48edf67ebe3a22bd5 Pdf

Convergence or Divergence of P1 n=1 an If Sn!N2 en (II) X1 n=1 2n1 2n 1 n Solution (I) Notice (n 1)! The Attempt at a Solution lim n^2/ (n^3n^2) =lim 1/n Therefore intuitively it should diverge like 1/n However, I am not very good at the Big O Small O notation Can someone show me 1 A proof without using Big O or Small O , but purely epsilon delta, for all n>N type of argument 2

Chapter 10

Divergence Test Determining If A Series Converges Or Diverges Owlcation

If they do not, the series will not converge Looking back, we can apply this theorem to the series in Example 1 In that example, the \(n^\text{th}\) terms of both sequences do not converge to 0, therefore we can quickly conclude that each series diverges Important!I used Divergence Test and I'm stuck on this part #lim_(n>oo) (5/4)^n/(3/4)^n 1# Im having trouble finding the limit Calculus Tests of Convergence / Divergence Strategies to Test an Infinite Series for Convergence 2 Answers Andrea SFree Series Divergence Test Calculator Check divergennce of series usinng the divergence test stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy

Sigma 2 Infinity N 2 1 N 3 1 Determine Whether The Series Converges Or Diverges Youtube

Solutions To Stewart Calculus Early Transcendentals Pg 726 Ex 23 Homework Help And Answers Slader

When does the sequence for math2^n/math diverge or converge?( n1) 2n 3n converges absolutely (4) See (4) (5) See (3) (1) is true 3 Determine if the two series diverge, converge conditionally, or converge absolutely (I) X1 n=1 ( 1)n(n1)!149 The following series are telescoping (although it may not appear so at first glance) For each series, determine if it is convergent or divergent, and calculate its value if it converges (Hint partial fractions may be useful in some parts)

Determine The Convergence Or Divergence Of F N N2 N 1 N2 1 N Stumbling Robot

Calculus Find The Radius Of Convergence For 3n Online Presentation

Does the series $\sum n!/n^n$ converge or diverge? You appear to be on a device with a "narrow" screen width (ie you are probably on a mobile phone)Due to the nature of the mathematics on this site it isDetermine the convergence or divergence of 1 1

N 3 3 N Series Convergence Youtube

Determine Whether The Series Converges Or Diverges Chegg Com

 a) The series diverges because it is geometric with r = 5/4 and a = –1 b) The series converges to 4 because it is Math Does the following infinite geometric series diverge or converge?Answer "Converges" Or "Diverges" A_n = 4 (1)^3n A_n = (7/8)^n A_n = 2^n/3^n 1 sigma(1, infinity) (4 3^n)/2^n Determine whether the series converges or diverges

Oneclass Determine Whether The Sequence Converges Or Diverges A N Cos 2 N 3 N

1 State And Prove Divergence Or Convergence For Each Chegg Com

2n 3n = 2 3 n Therefore, X1 n=0 2n 3n n3 < X1 n=0 2 3 n = 1 1 2 3 = 3 Hence, the given series converges 2Does the following series converge or diverge?(a) Only (I) and (III) converge (b) Only(III) converges (c) Only (I) and (II) converge (d)All three converge (e) All three diverge Solution Here the correct answer is only (I) and (III) converge Let b n = p1 n Then b n > 0, b n is decreasing and lim n!1b n = 0Hence by the alternating series test the series P 1 n=2 ( 1)n p convergesIt has a sum*** C) It diverges;

Sigma 1 Infinity 2 N 1 3 N Determine Whether The Series Converges Or Diverges Youtube

Web Northeastern Edu Suciu Mth1125 1125sp02 Sol3 Pdf

1 3 If 0 < x < 1;1 Does the series converge or diverge {eq}\sum_{n = 1}^{\infty} \frac{\ln(n 1) \sin n}{n^{32}} {/eq} 2 Evaluate the sum {eq}\sum_{n = 0}^{\infty} \frac{2^nExplain 3 9 27 81 A) It diverges;

Ratio Test Video Khan Academy

Determine If The Sequence Frac 3 N N 3 1 Converges Or Diverges Mathematics Stack Exchange

1Determine if the following series converge or diverge If the series converges, also compute the sum You must show all of your work and support your conclusions (a)(7 points) X1 n=0 2n 1 3n Solution X1 n=0 2n 1 3n = 1 n=0 2 2 2n 1 3n = X1 n=0 1 2 2n 3n = 1 2 X1 n=0 2 3 n = 1 2 1 1 2=3 = 3 2 And so the series is a geometric with jrj= 2=3Converge, and which diverge? lim_(n>oo) a_n = 1 Divide both numerator and denominator by 3^n like this lim_(n>oo) a_n = lim_(n>oo) (2^n3^n)/(2^n3^n) color(white)(lim_(n>oo) a_n) = lim_(n>oo) ((2/3)^n1)/((2/3)^n1) color(white)(lim_(n>oo) a_n) = (01)/(01) color(white)(lim_(n>oo) a_n) = 1

2 Determine Whether The Following Series Converge Or Chegg Com

2 Prove Whether The Following Series Converge Or Chegg Com

It does not have a sum B) It converges;(3(n2)2n)/3n By signing up, you'll get thousands of stepbystep solutions to your homeworkMidterm Math 143 (Calculus III) 2 (16 points) Determine if each series converges or diverges If the series converges, calculate the exact value to which it converges

Math 2260 Exam 3 Practice Problem Solutions

Direct And Limit Comparison Test Ppt Download

 for every integer n ≥ 2 and ∑ ∞ n = 21 / n diverges, we have that ∑ ∞ n = 2 1 lnn diverges Exercise 841 Use the comparison test to determine if the series ∑ ∞ n = 1 n n3 n 1 converges or diverges Hint Find a value p such that n n

Answered Series 23 56 Determine Whether The Bartleby

Www Colorado Edu Amath Sites Default Files Attached Files Archive Appm1360summer19exam3 Sol Pdf

Geneseo Math 222 01 Absolute Convergence

Sequences And Series Pdf Free Download

Lim N Oo Sqrt N 3 2n 2 1 3sqrt N 4 1 3 4sqrt N 6 6n 5 2

Pdf Tests For Convergence Of Series Diego Guevara And Diego Medina Ramirez Academia Edu

Answered In Exercises Converges Or Diverges Bartleby

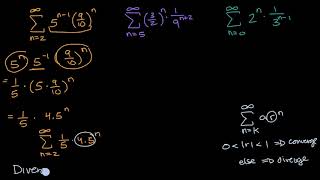
Convergent Divergent Geometric Series With Manipulation Video Khan Academy

2 Determine Whether The Following Series Converge Or Diverge A 1 Imim8 N 3 N 2 N Homeworklib

An 1 N N 3 N 3 2n 2 1 Determine Whether The Sequence Converges Or Diverges Youtube

1

Calculus Find The Radius Of Convergence For 3n Online Presentation

Teachingcenter Ufl Edu Files Exam 2 Review Problems Mac 2312 Pdf

Http Edshare Soton Ac Uk Id Document 5512

What Is The Convergence Of The Series 1 3 N Quora

Q3 Determine Wither The Following Series Are Converge Or Diverge Gao In N 3 N Inn A In 1 Homeworklib

Mth3101 Advanced Calculus Chapter 3

Www3 Nd Edu Taylor Math Oldexams Exam3b Pdf

Determine Whether The Series Is Convergent Or Divergent By Expressing Sn As A Telescoping Sum As In Brainly Com

If A N 1 Frac 3 A N 2 A N 1 And A 1 1 Then What Is Lim Limits N To Infty Left Frac 4 3 Right N 3 A N Mathematics Stack Exchange

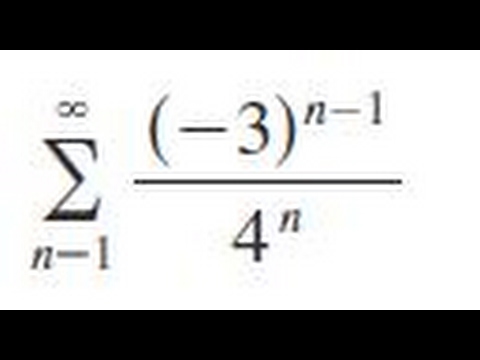
Sigma N 1 Infinity 3 N 1 4 N Youtube

Divergence Test Determining If A Series Converges Or Diverges Owlcation

Determine If The Series Convergence Or Divergence And State The Test Used 1 Sigma On Top Infinity When N 1 5 2n 1 2 Sigma On Top Infinity When N 1 2 4 6 2n N Homeworklib

Teachingcenter Ufl Edu Files Exam 2 Review Problems Mac 2312 Pdf

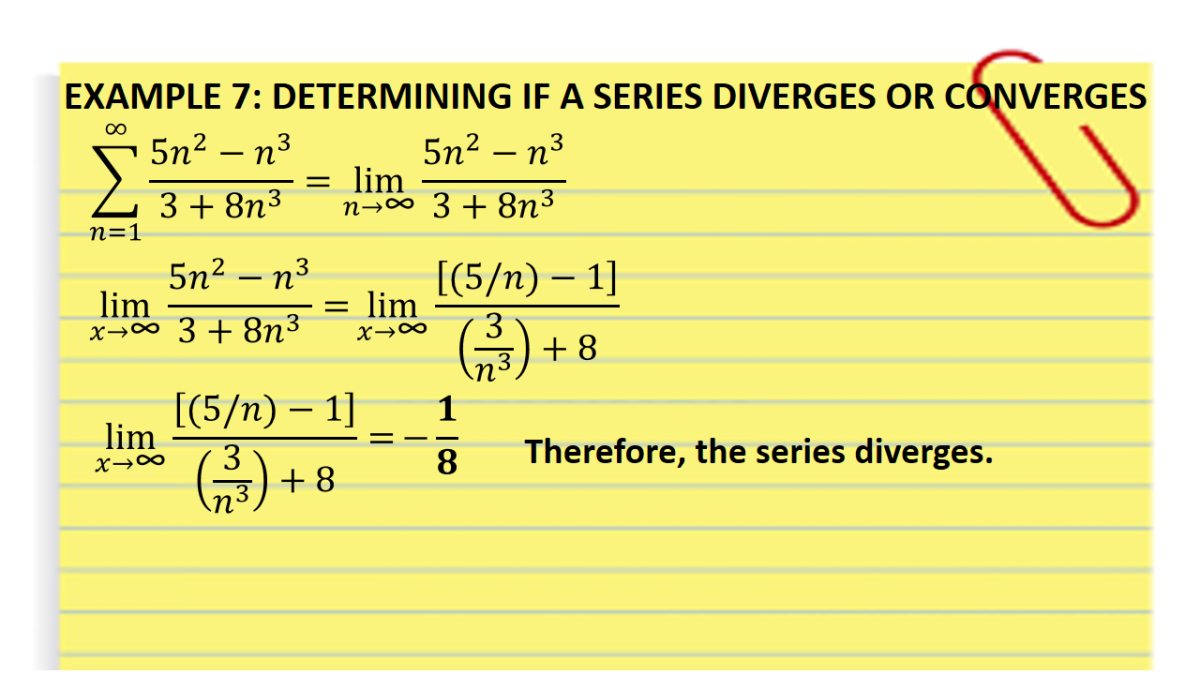
Divergence Test Determining If A Series Converges Or Diverges Owlcation

Answered Ries Diverges 23 56 Determine Whether Bartleby

Ism Et Chapter 8

Convergence And Divergence Calculus 2

Solved Use The Limit Comparison Test To Check The Convergence Of The Series N 1 2 N 3 N 2 6 N 5 3 N 2 Explain What Series You Are Comparing Course Hero

Teachingcenter Ufl Edu Files Exam 2 Review Problems Mac 2312 Pdf

Does Sum Limits N 3 Infty Frac Pi Left 3 Right N 1 7 N Converge Diverge Mathematics Stack Exchange

Limit Comparison Test Video Khan Academy

A Determine Whether The Sequence A N 2n N Chegg Com

Answered In Exercises 1 8 Use The Ratio Test To Bartleby

I Don T Understand This Explanation For Sum N 0 Infty 1 N 5n 1 Why Test For Convergence Divergence Again If The Limit Comparison Test Confirms That Both Series Are The Same Socratic

Will Series N N 1 Converge Or Diverge As N Tends To Infinity Quora

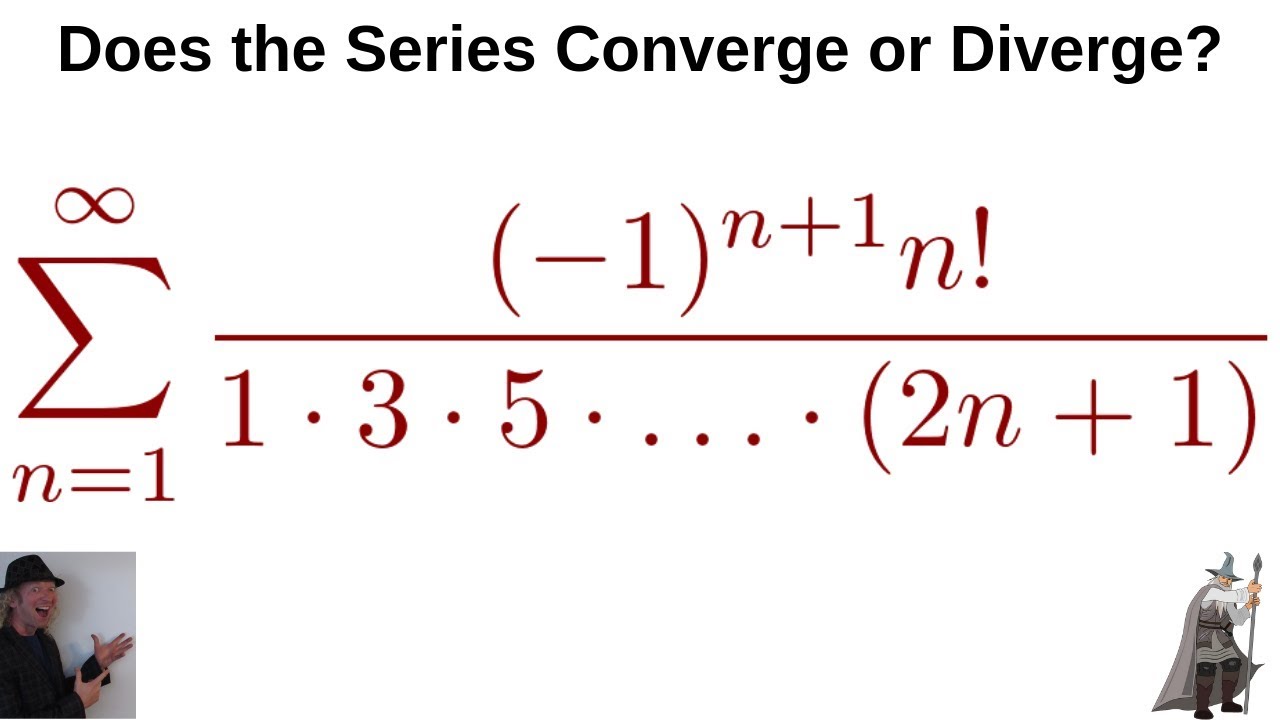
Infinite Series Sum 1 N 1 N 1 3 5 2n 1 Convergence Using The Ratio Test Youtube

Will Series N N 1 Converge Or Diverge As N Tends To Infinity Quora

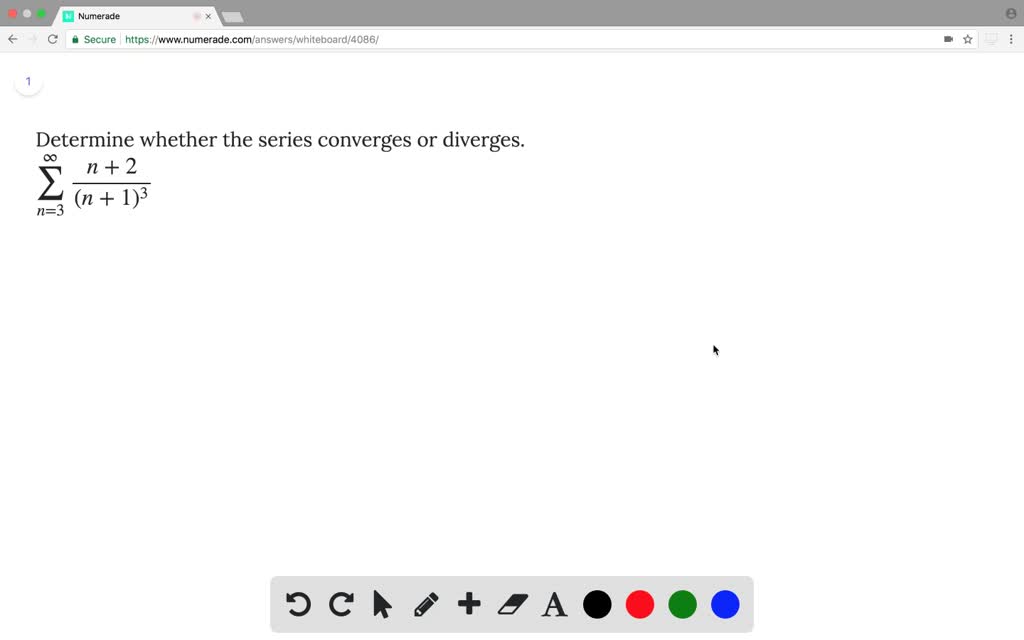
Solved Determine Whether The Series Converges Or

I Don T Understand This Explanation For Sum N 0 Infty 1 N 5n 1 Why Test For Convergence Divergence Again If The Limit Comparison Test Confirms That Both Series Are The Same Socratic

Find The Sum Of The Series Sum N 1 Infty Frac 3n 2 N Mathematics Stack Exchange

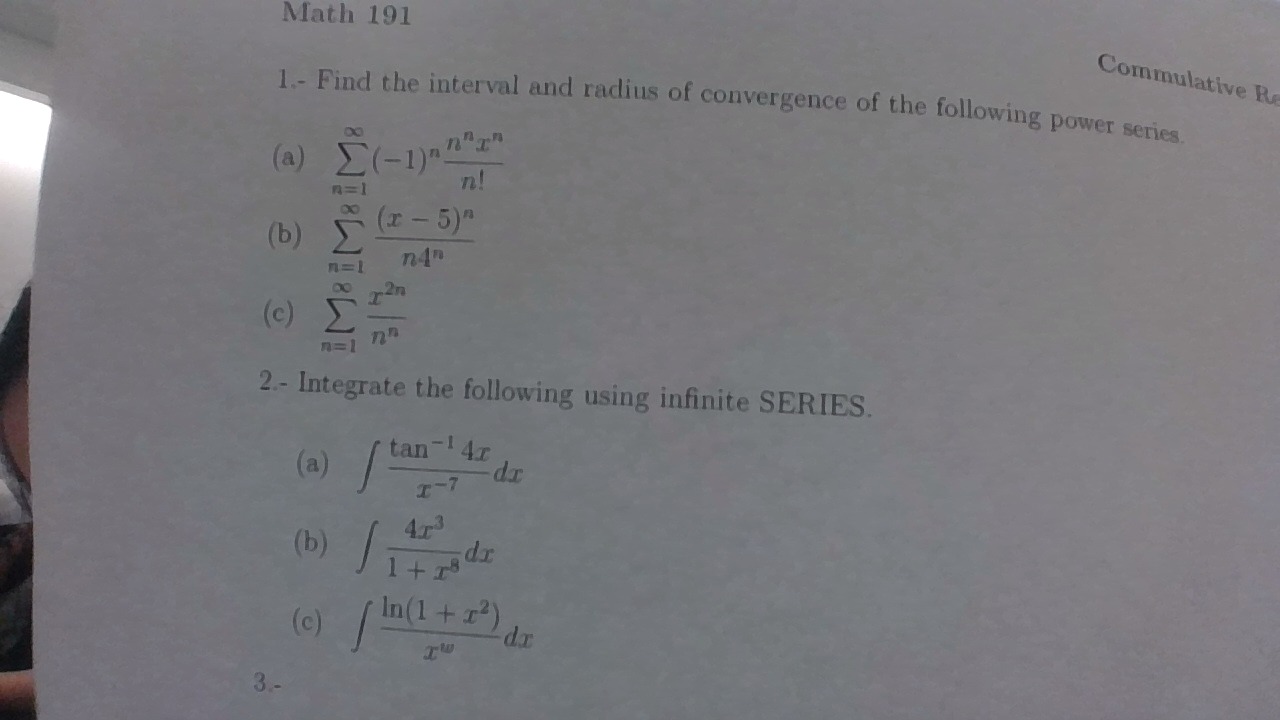
Find The Interval Radius Of Convergence For The Power Series In 1b Socratic

2

Series And Convergence Ppt Download

1 Let An 2n 3n 1 A Determine Whether An Chegg Com

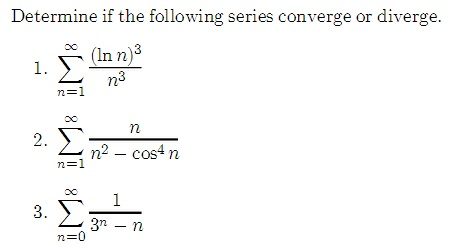
Determine If The Following Series Converge Or Chegg Com

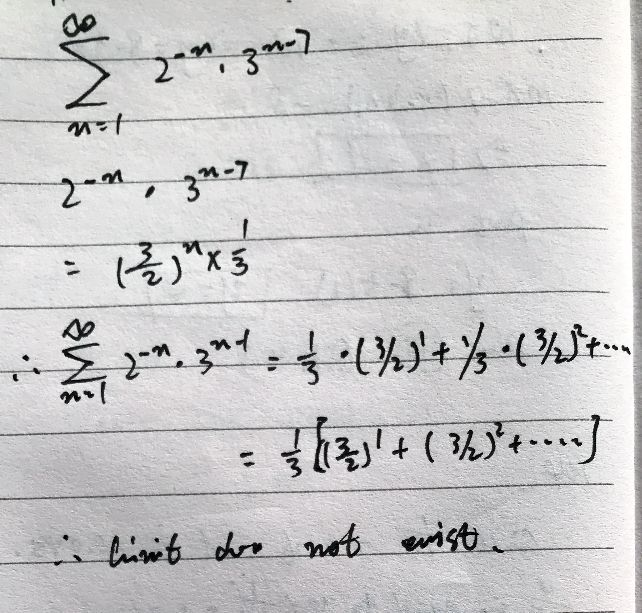
Determine Whether The Series Sum Limits N 1 Infty 2 N 3 N 1 Converges Or Diverges If It Onverges Find Its Limit Snapsolve

Alternating Series

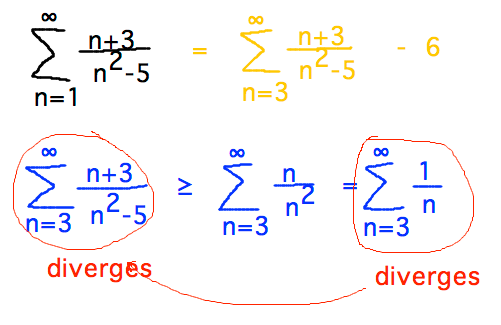
Geneseo Math 222 01 Absolute Convergence

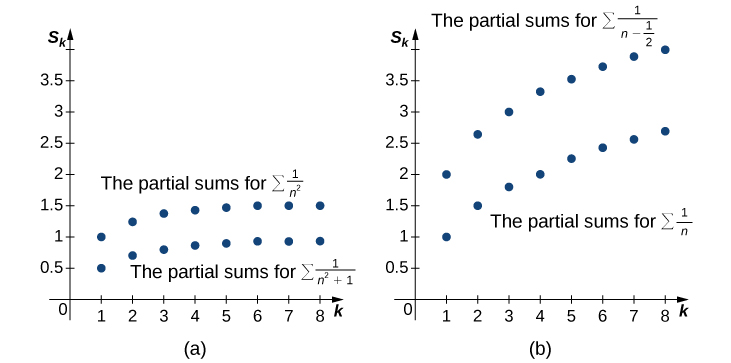
8 4 Convergence Tests Comparison Test Mathematics Libretexts

Www2 Kenyon Edu Depts Math Kalaycioglu Calculus b Testsforconvergencewithanswers Pdf

1

Sequences And Series Pdf Free Download

1 Determine Whether The Series Converge Or Diverge Chegg Com

If A N 1 Frac 3 A N 2 A N 1 And A 1 1 Then What Is Lim Limits N To Infty Left Frac 4 3 Right N 3 A N Mathematics Stack Exchange

An 3 N N Determine Whether The Sequence Converges Or Diverges Youtube

Www Ualberta Ca Rjia Math214 Hwks Sol2 Pdf

Divergence Test Determining If A Series Converges Or Diverges Owlcation

1

Http Www Math Colostate Edu Clayton Teaching M115f09 Exams Exam1solutions Pdf

Absolute And Conditional Convergence

Limit Comparison Test For Series 1 N 2 Log N Converge Or Diverge Mathematics Stack Exchange

5 Test For Convergence Divergence 15 Pts 13n 2n 4 A Nº N 3 N 1 Homeworklib

Determine Whether Each Series Converges Or Diverges Chegg Com

The Sum Of The Infinite And Finite Geometric

1

Use The Ratio Test To Find Which Of The Following Chegg Com

Answers To The Tests For Convergence Practice Worksheet

Incoming Term: 2^n/3^n converge or diverge, n^2/(n^3+1) convergent or divergent, 3^(n+2)/5^n converge or diverge, does (2/3)^n converge or diverge, does 1/3^n converge or diverge, does 2^n/3^n converge, does ne^-n converge or diverge, does 1/n^2 converge or diverge,